Principles of datashading¶

Because HoloViews elements are fundamentally data containers, not visualizations, you can very quickly declare elements such as Points or Path containing datasets that may be as large as the full memory available on your machine (or even larger if using Dask dataframes). So even for very large datasets, you can easily specify a data structure that you can work with for making selections, sampling, aggregations, and so on. However, as soon as you try to visualize it directly with either the matplotlib or bokeh plotting extensions, the rendering process may be prohibitively expensive.

Let's start with a simple example we can visualize as normal:

These browser-based plots are fully interactive, as you can see if you select the Wheel Zoom or Box Zoom tools and use your scroll wheel or click and drag.

Because all of the data in these plots gets transferred directly into the web browser, the interactive functionality will be available even on a static export of this figure as a web page. Note that even though the visualization above is not computationally expensive, even with just 1000 points as in the scatterplot above, the plot already suffers from overplotting, with later points obscuring previously plotted points.

With much larger datasets, these issues will quickly make it impossible to see the true structure of the data. We can easily declare 50X or 1000X larger versions of the same plots above, but if we tried to visualize them they would be nearly unusable even if the browser did not crash:

Luckily, HoloViews Elements are just containers for data and associated metadata, not plots, so HoloViews can generate entirely different types of visualizations from the same data structure when appropriate. For instance, in the plot on the left below you can see the result of applying a decimate() operation acting on the points object, which will automatically downsample this million-point dataset to at most 1000 points at any time as you zoom in or out:

Decimating a plot in this way can be useful, but it discards most of the data, yet still suffers from overplotting. If you have Datashader installed, you can instead use the datashade() operation to create a dynamic Datashader-based Bokeh plot. The middle plot above shows the result of using datashade() to create a dynamic Datashader-based plot out of an Element with arbitrarily large data. In the Datashader version, a new image is regenerated automatically on every zoom or pan event, revealing all the data available at that zoom level and avoiding issues with overplotting by dynamically rescaling the colors used. The same process is used for the line-based data in the Paths plot.

These two Datashader-based plots are similar to the native Bokeh plots above, but instead of making a static Bokeh plot that embeds points or line segments directly into the browser, HoloViews sets up a Bokeh plot with dynamic callbacks that render the data as an RGB image using Datashader instead. The dynamic re-rendering provides an interactive user experience even though the data itself is never provided directly to the browser. Of course, because the full data is not in the browser, a static export of this page (e.g. on holoviews.org or on anaconda.org) will only show the initially rendered version, and will not update with new images when zooming as it will when there is a live Python process available.

Though you can no longer have a completely interactive exported file, with the Datashader version on a live server you can now change the number of data points from 1000000 to 10000000 or more to see how well your machine will handle larger datasets. It will get a bit slower, but if you have enough memory, it should still be very usable, and should never crash your browser as transferring the whole dataset into your browser would. If you don't have enough memory, you can instead set up a Dask dataframe as shown in other Datashader examples, which will provide out-of-core and/or distributed processing to handle even the largest datasets.

The datashade() operation is actually a "macro" or shortcut that combines the two main computations done by datashader, namely shade() and rasterize():

In all three of the above plots, rasterize() is being called to aggregate the data (a large set of x,y locations) into a rectangular grid, with each grid cell counting up the number of points that fall into it. In the plot on the left, only rasterize() is done, and the resulting numeric array of counts is passed to Bokeh for colormapping. Bokeh can then use dynamic (client-side, browser-based) operations in JavaScript, allowing users to have dynamic control over even static HTML plots. For instance, in this case, users can use the Box Select tool and select a range of the histogram shown, dynamically remapping the colors used in the plot to cover the selected range.

The other two plots should be identical. In both cases, the numerical array output of rasterize() is mapped into RGB colors by Datashader itself, in Python ("server-side"), which allows special Datashader computations like the histogram-equalization in the above plots and the "spreading" discussed below. The shade() and datashade() operations accept a cmap argument that lets you control the colormap used, which can be selected to match the HoloViews/Bokeh cmap option but is strictly independent of it. See hv.help(rasterize), hv.help(shade), and hv.help(datashade) for options that can be selected, and the Datashader web site for all the details. The lower-level aggregate() and regrid() give more control over how the data is aggregated.

Since datashader only sends the data currently in view to the plotting backend, the default behavior is to rescale colormap to the range of the visible data as the zoom level changes. This behavior may not be desirable when working with images; to instead use a fixed colormap range, the clim parameter can be passed to the bokeh backend via the opts() method. Note that this approach works with rasterize() where the colormapping is done by the bokeh backend. With datashade(), the colormapping is done with the shade() function which takes a clims parameter directly instead of passing additional parameters to the backend via opts().

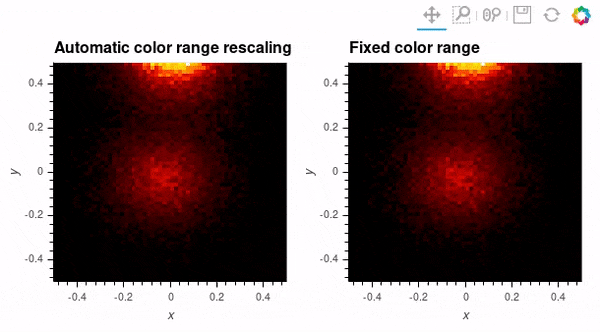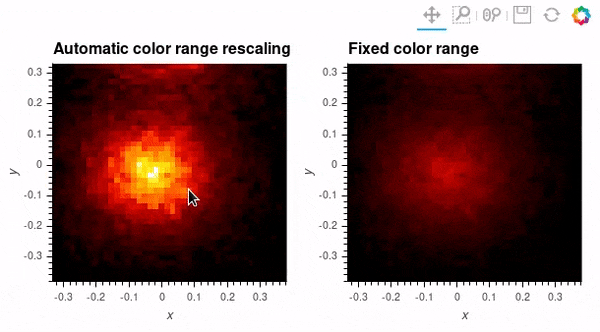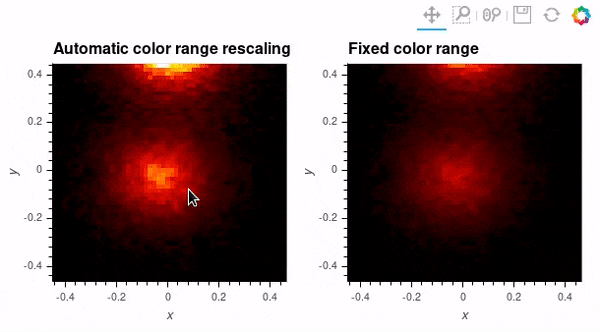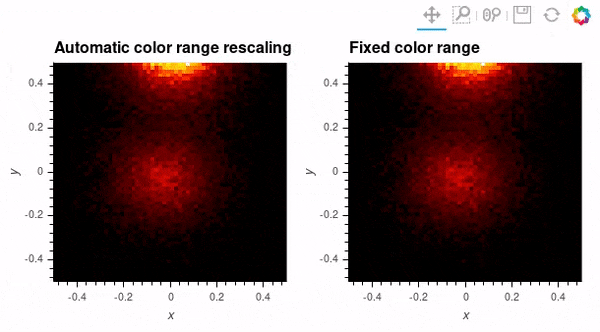
Spreading¶

The Datashader examples above treat points and lines as infinitesimal in width, such that a given point or small bit of line segment appears in at most one pixel. This approach ensures that the overall distribution of the points will be mathematically well founded -- each pixel will scale in value directly by the number of points that fall into it, or by the lines that cross it.

However, many monitors are sufficiently high resolution that the resulting point or line can be difficult to see---a single pixel may not actually be visible on its own, and its color may likely be very difficult to make out. To compensate for this, HoloViews provides access to Datashader's image-based "spreading", which makes isolated pixels "spread" into adjacent ones for visibility. There are two varieties of spreading supported:

1. spread: fixed spreading of a certain number of pixels, which is useful if you want to be sure how much spreading is done regardless of the properties of the data.
2. dynspread: spreads up to a maximum size as long as it does not exceed a specified fraction of adjacency between pixels.

Dynamic spreading is typically more useful, because it adjusts depending on how close the datapoints are to each other on screen. Both types of spreading require Datashader to do the colormapping (applying shade), because they operate on RGB pixels, not data arrays.

You can compare the results in the two plots below after zooming in:

Both plots show the same data, and look identical when zoomed out, but when zoomed in enough you should be able to see the individual data points on the right while the ones on the left are barely visible. The dynspread parameters typically need some hand tuning, as the only purpose of such spreading is to make things visible on a particular monitor for a particular observer; the underlying mathematical operations in Datashader do not normally need parameters to be adjusted.

The same operation works similarly for line segments:

Multidimensional plots¶

The above plots show two dimensions of data plotted along x and y, but Datashader operations can be used with additional dimensions as well. For instance, an extra dimension (here called k), can be treated as a category label and used to colorize the points or lines, aggregating the data points separately depending on which category value they have. Compared to a standard overlaid scatterplot that would suffer from overplotting, here the result will be merged mathematically by Datashader, completely avoiding any overplotting issues except any local issues that may arise from spreading when zoomed in:

Above you can see that (as of Datashader 0.11) categorical aggregates can take any reduction function, either counting the datapoints (left) or reporting some other statistic (e.g. the mean value of a column, right).

Categorical aggregates are one way to allow separate lines or other shapes to be visually distinctive from one another while avoiding obscuring data due to overplotting:

Note that Bokeh only ever sees an image come out of hd.datashade, not any of the actual data. As a result, providing legends and keys has to be done separately, though we are working to make this process more seamless. For now, you can show a legend by adding a suitable collection of "fake" labeled points (size zero and thus invisible):

Here the dummy points are at 0,0 for this dataset, but would need to be at another suitable value for data that is in a different range.

Working with time series¶

HoloViews also makes it possible to datashade large timeseries using the datashade and rasterize operations:

HoloViews also supplies some operations that are useful in combination with Datashader timeseries. For instance, you can compute a rolling mean of the results and then show a subset of outlier points, which will then support hover, selection, and other interactive Bokeh features:

Note that the above plot will look blocky in a static export (such as on anaconda.org), because the exported version is generated without taking the size of the actual plot (using default height and width for Datashader) into account, whereas the live notebook automatically regenerates the plot to match the visible area on the page. The result of all these operations can be laid out, overlaid, selected, and sampled just like any other HoloViews element, letting you work naturally with even very large datasets.

Hover info¶

As you can see in the examples above, converting the data to an image using Datashader makes it feasible to work with even very large datasets interactively. One unfortunate side effect is that the original datapoints and line segments can no longer be used to support "tooltips" or "hover" information directly for RGB images generated with datashade; that data simply is not present at the browser level, and so the browser cannot unambiguously report information about any specific datapoint.

If you do need hover information, there are two good options available:

1) Use the rasterize operation without shade, which will let the plotting code handle the conversion to colors while still having the actual aggregated data to support hovering

2) Overlay a separate layer as a QuadMesh or Image containing the hover information

In the above examples, the plot on the left provides hover information directly on the aggregated Image. The middle plot displays hover information as a QuadMesh at a fixed spatial scale, while the one on the right reports on an area that scales with the zoom level so that arbitrarily small regions of data space can be examined, which is generally more useful (but requires a live Python server).

Element types supported for Datashading¶

Fundamentally, what datashader does is to rasterize data, i.e., render a representation of it into a regularly gridded rectangular portion of a two-dimensional plane. Datashader natively supports six basic types of rasterization:

• points: zero-dimensional objects aggregated by position alone, each point covering zero area in the plane and thus falling into exactly one grid cell of the resulting array (if the point is within the bounds being aggregated).
• line: polyline/multiline objects (connected series of line segments), with each segment having a fixed length but zero width and crossing each grid cell at most once.
• area: a region to fill either between the supplied y-values and the origin or between two supplied lines
• trimesh: irregularly spaced triangular grid, with each triangle covering a portion of the 2D plane and thus potentially crossing multiple grid cells (thus requiring interpolation/upsampling). Depending on the zoom level, a single pixel can also include multiple triangles, which then becomes similar to the points case (requiring aggregation/downsampling of all triangles covered by the pixel).
• raster: an axis-aligned regularly gridded two-dimensional subregion of the plane, with each grid cell in the source data covering more than one grid cell in the output grid (requiring interpolation/upsampling), or with each grid cell in the output grid including contributions from more than one grid cell in the input grid (requiring aggregation/downsampling).
• quadmesh: a recti-linear or curvi-linear mesh (like a raster, but allowing nonuniform spacing and coordinate mapping) where each quad can cover one or more cells in the output (requiring upsampling, currently only as nearest neighbor), or with each output grid cell including contributions from more than one input grid cell (requiring aggregation/downsampling).
• polygons: arbitrary filled shapes in 2D space (bounded by a piecewise linear set of segments), optionally punctuated by similarly bounded internal holes

Datashader focuses on implementing those four cases very efficiently, and HoloViews in turn can use them to render a very large range of specific types of data:

Supported Elements¶

• points: hv.Nodes, hv.Points, hv.Scatter
• line: hv.Contours, hv.Curve, hv.Path, hv.Graph, hv.EdgePaths, hv.Spikes, hv.Segments
• area: hv.Area, hv.Spread
• raster: hv.Image, hv.HSV, hv.RGB
• trimesh: hv.TriMesh
• quadmesh: hv.QuadMesh
• polygons: hv.Polygons

Other HoloViews elements could be supported, but do not currently have a useful datashaded representation:

Elements not yet supported¶

• line: hv.Spline, hv.VectorField
• raster: hv.HeatMap, hv.Raster

There are also other Elements that are not expected to be useful with datashader because they are isolated annotations, are already summaries or aggregations of other data, have graphical representations that are only meaningful at a certain size, or are text based:

Not useful to support¶

• datashadable annotations: hv.Arrow, hv.Bounds, hv.Box, hv.Ellipse (actually do work with datashade currently, but not officially supported because they are not vectorized and thus unlikely to have enough items to be worth datashading)
• other annotations: hv.Arrow, hv.HLine, hv.VLine, hv.Text
• kdes: hv.Distribution, hv.Bivariate
• categorical/symbolic: hv.BoxWhisker, hv.Bars, hv.ErrorBars
• tables: hv.Table, hv.ItemTable

Examples of each supported Element type:

Here we called datashade() on each Element type, letting Datashader do the full process of rasterization and shading, except that for RGB and HSV we only called rasterize() or else the results would have been converted into a monochrome image.

For comparison, you can see the corresponding non-datashaded plots (as long as you leave N lower than 10000 unless you have a long time to wait!):

These two examples use Matplotlib, but if they were switched to Bokeh and you had a live server, they would support dynamic re-rendering on zoom and pan so that you could explore the full range of data available (e.g. even very large raster images, networks, paths, point clouds, or meshes).

Container types supported for datashading¶

In the above examples datashade() was called directly on each Element, but it can also be called on Containers, in which case each Element in the Container will be datashaded separately (for all Container types other than a Layout):

Optimizing performance¶

Datashader and HoloViews have different design principles that are worth keeping in mind when using them in combination, if you want to ensure good overall performance. By design, Datashader supports only a small number of operations and datatypes, focusing only on what can be implemented very efficiently. HoloViews instead focuses on supporting the typical workflows of Python users, recognizing that the most computationally efficient choice is only going to be faster overall if it also minimizes the time users have to spend getting things working.

HoloViews thus helps you get something working quickly, but once it is working and you realize that you need to do this often or that it comes up against the limits of your computing hardware, you can consider whether you can get much better performance by considering the following issues and suggestions.

Use a Datashader-supported data structure¶

HoloViews helpfully tries to convert whatever data you have provided into what Datashader supports, which is good for optimizing your time to an initial solution, but will not always be the fastest approach computationally. If you ensure that you store your data in a format that Datashader understands already, HoloViews can simply pass it down to Datashader without copying or transforming it:

1. For point, line, and trimesh data, Datashader supports Dask and Pandas dataframes, and so those two data sources will be fastest. Of those two, Dask Dataframes will usually be somewhat faster and also able to make use of distributed computational resources and out-of-core processing.
2. For rasters and quadmeshes, Datashader supports xarray objects natively, and so if your data is provided as an xarray already, plotting will be faster.
3. For polygons Datashader supports spatialpandas DataFrames.

See the Datashader docs for examples of dealing with even quite large datasets (in the billions of points) on commodity hardware, including many HoloViews-based examples.

Cache initial processing with precompute=True¶

In the typical case of having datasets much larger than the plot resolution, HoloViews Datashader-based operations that work on the full dataset (rasterize, aggregate,regrid) are computationally expensive; the others are not (shade, spread, dynspread, etc.)

The expensive operations are all of type ResamplingOperation, which has a parameter precompute (see hv.help(hv.operation.datashader.rasterize), etc.) Precompute can be used to get faster performance in interactive usage by caching the last set of data used in plotting (after any transformations needed) and reusing it when it is requested again. This is particularly useful when your data is not in one of the supported data formats already and needs to be converted. precompute is False by default, because it requires using memory to store the cached data, but if you have enough memory, you can enable it so that repeated interactions (such as zooming and panning) will be much faster than the first one. In practice, most Datashader-plots don't need to do extensive precomputing, but enabling it for TriMesh and Polygon plots can greatly speed up interactive usage.

Use GPU support¶

Many elements now also support aggregation directly on a GPU-based datastructure such as a cuDF DataFrame or an Xarray DataArray backed by a cupy array. These data structures can be passed directly to the appropriate HoloViews elements just as you would use a Pandas or other Xarray object. For instance, a cuDF can be used on elements like hv.Points and hv.Curve, while a cupy-backed DataArray raster or quadmesh can be passed to hv.QuadMesh elements. When used with Datashader, the GPU implementation can result in 10-100x speedups, as well as avoiding having to transfer the data out of the GPU for plotting (sending only the final rendered plot out of the GPU's memory). To see which HoloViews elements are supported, see the datashader performance guide. As of the Datashader 0.11 release, all point, line, area, and quadmesh aggregations are supported when using a GPU backed datastructure, including raster objects like hv.Image if first converted to hv.Quadmesh.

Project data only once¶

If you are working with geographic data using GeoViews that needs to be projected before display and/or before datashading, GeoViews will have to do this every time you update a plot, which can drown out the performance improvement you get by using Datashader. GeoViews allows you to project the entire dataset at once using gv.operation.project, and once you do this you should be able to use Datashader at full speed.

If you follow these suggestions, the combination of HoloViews and Datashader will allow you to work uniformly with data covering a huge range of sizes. Per session or per plot, you can trade off the ability to export user-manipulable plots against file size and browser compatibility, and allowing you to render even the largest dataset faithfully. HoloViews makes the full power of Datashader available in just a few lines of code, giving you a natural way to work with your data regardless of its size.